Resolución de Sistemas de Ecuaciones Lineales: Método Gauss-Jordan Paso a Paso

Introducción

Como trabajo final para el régimen de promoción de la asignatura Matemática I, se presenta esta monografía referida a la resolución de sistemas de ecuaciones lineales por el método de Gauss-Jordan.

Tras buscar y seleccionar la información pertinente y realizar un repaso general sobre matrices y ecuaciones lineales, estamos en condiciones de elaborar este documento conforme a los requisitos propuestos por la cátedra durante el cursado.

Desarrollo del Método de Gauss-Jordan

¿Qué es el Método de Gauss-Jordan?

El Método de Gauss-Jordan, también llamado eliminación de Gauss-Jordan, es un algoritmo del álgebra lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices inversas y resolver otros problemas relacionados. En este documento, nos centraremos en su aplicación para resolver sistemas de ecuaciones lineales con n variables.

Pasos para Resolver Sistemas de Ecuaciones

Para resolver sistemas de ecuaciones lineales aplicando este método, se siguen fundamentalmente estos pasos:

1. Notación Matricial (Matriz Aumentada)

Se deben anotar los coeficientes de las variables y los términos independientes del sistema de ecuaciones lineales en su notación matricial. Si el sistema es:

Se representa como una matriz aumentada:

2. Transformación a Matriz Identidad

A continuación, se procede a transformar dicha matriz aumentada en una forma escalonada reducida por filas, que idealmente (si la solución es única) será la matriz identidad en la parte de los coeficientes. La forma final buscada es:

Esto se logra aplicando operaciones elementales por fila a la matriz aumentada. Estas operaciones incluyen:

• Intercambiar dos filas.
• Multiplicar una fila por un escalar no nulo.
• Sumar a una fila un múltiplo de otra fila.

Importante: Cada operación se aplica a todos los elementos de la fila correspondiente.

3. Interpretación de la Solución

Una vez que la parte izquierda de la matriz aumentada (correspondiente a los coeficientes) se ha transformado en la matriz identidad, la columna de la derecha (originalmente los términos independientes) contendrá las soluciones del sistema. Es decir, los valores resultantes verificarán la igualdad para cada una de las variables, correspondiéndose de la siguiente forma:

• d1 = x
• d2 = y
• d3 = z
• ... y así sucesivamente para más variables.

Ejemplo Práctico Detallado

Ahora que están sentadas las bases, podemos explicar paso a paso la resolución con un ejemplo concreto.

• Sea el sistema de ecuaciones:

Paso 1: Escribir la Matriz Aumentada

Procedemos a anotarlo en su forma matricial:

Una vez hecho esto, podemos empezar a operar con las distintas filas de la matriz para transformarla hasta que la parte izquierda sea la matriz identidad:

Paso 2: Obtener el primer '1' (Pivote en Fila 1, Columna 1)

Lo primero que debemos hacer es transformar el 2 en la posición (1,1) de la matriz original en el 1 de la matriz identidad. Para hacer esto, multiplicamos toda la 1ª fila (F1) por el inverso de 2, es decir, 1/2.

Operación: F1 = (1/2) * F1

Paso 3: Obtener ceros debajo del primer pivote

Luego, debemos obtener los dos ceros en la primera columna, debajo del '1' que acabamos de conseguir. Para lograr esto, buscamos el opuesto de los números en esas posiciones: el opuesto de 3 (posición 2,1) es -3, y el opuesto de 5 (posición 3,1) es -5.

Realizamos las siguientes operaciones:

• A la Fila 2 (F2) le sumamos la Fila 1 multiplicada por -3. Operación: F2 = F2 - 3 * F1
• A la Fila 3 (F3) le sumamos la Fila 1 multiplicada por -5. Operación: F3 = F3 - 5 * F1

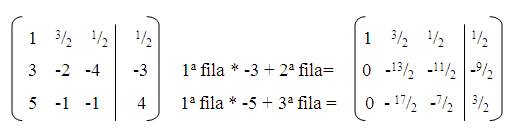
Paso 4: Obtener el segundo '1' (Pivote en Fila 2, Columna 2)

Nuestro siguiente paso es obtener el '1' en la posición (2,2) de la matriz identidad. Procedemos de igual forma que antes: multiplicamos toda la Fila 2 por el inverso del número en esa posición, que es -13/2. Su inverso es -2/13.

Operación: F2 = (-2/13) * F2

Nota opcional: Si observamos la tercera fila (-17/2, -7/2, 3/2), nos damos cuenta de que todos los elementos tienen denominador 2. Podemos simplificar los cálculos multiplicando toda la Fila 3 por 2. Esto no es estrictamente necesario, pero facilita las operaciones. Operación (opcional): F3 = 2 * F3. La siguiente imagen muestra el resultado después de aplicar ambas operaciones (la de F2 y la simplificación de F3).

Paso 5: Obtener cero debajo del segundo pivote

Ahora queremos obtener el 0 que se ubica en la posición (3,2). Buscamos el opuesto del número que está en esa posición en la matriz actual (-17), cuyo opuesto es 17. Multiplicamos la Fila 2 por 17 y la sumamos a la Fila 3.

Operación: F3 = F3 + 17 * F2

A esta altura podemos observar cómo la matriz con la cual estamos operando empieza a parecerse a la matriz identidad en su parte izquierda.

Paso 6: Obtener el tercer '1' (Pivote en Fila 3, Columna 3)

Nuestro siguiente paso es obtener el '1' correspondiente a la posición (3,3). Aplicamos el mismo procedimiento: multiplicamos toda la Fila 3 por el inverso del número que se encuentre en esa posición (96/13), cuyo inverso es 13/96.

Operación: F3 = (13/96) * F3

Paso 7: Obtener ceros arriba del tercer pivote

Luego debemos obtener los dos ceros en la tercera columna, por encima del '1' que acabamos de conseguir (en las posiciones (1,3) y (2,3)). Buscamos los opuestos de los números que se ubican en esas posiciones: el opuesto de 1/2 es -1/2, y el opuesto de 11/13 es -11/13.

Realizamos las siguientes operaciones:

• A la Fila 1 (F1) le sumamos la Fila 3 multiplicada por -1/2. Operación: F1 = F1 - (1/2) * F3
• A la Fila 2 (F2) le sumamos la Fila 3 multiplicada por -11/13. Operación: F2 = F2 - (11/13) * F3

Paso 8: Obtener cero arriba del segundo pivote

El último paso que debemos realizar es obtener el 0 en la posición (1,2). Buscamos el opuesto del número que se ubica en esa posición (3/2), cuyo opuesto es -3/2. Multiplicamos la Fila 2 por -3/2 y la sumamos a la Fila 1.

Operación: F1 = F1 - (3/2) * F2

Paso 9: Interpretación de la Solución

Como podemos observar, hemos llegado al modelo de la matriz identidad en la parte izquierda. En la cuarta columna (la columna aumentada) hemos obtenido los valores de las variables, correspondiéndose de este modo:

x = 1

y = -1

z = 2

Paso 10: Verificación de la Solución

Finalmente, verificamos que estos valores satisfacen el sistema de ecuaciones original:

Sistema original:

2x + 3y + z = 1
3x – 2y – 4z = -3
5x – y – z = 4

Sustituyendo x=1, y=-1, z=2:

2*(1) + 3*(-1) + 2 = 2 - 3 + 2 = 1  (Correcto)
3*(1) – 2*(-1) – 4*(2) = 3 + 2 - 8 = -3 (Correcto)
5*(1) – (-1) – 2 = 5 + 1 - 2 = 4  (Correcto)

El sistema de ecuaciones está resuelto y verificado.